English
This month, I wanted to chill on writing about CTF’s, so instead I decided to look into a tool I often use during CTF contest, mainly for crypto challenges. The tool is the integer factorization calculator by Dario Alpern. This integer factorization calculator uses two different methods for factorization, the first being the Elliptic Curve Method (ECM), and the Self Initializing Quadratic Sieve (SIQS).
I decided to dig into the ECM algorithm, and in this post I also have python code that works, although not really pretty or fast.
How does it work?
The algorithm isn’t that hard, so I’m just gonna quote Wikipedia as that is where I learnt this algorithm.
Part 1: Elliptic curve
The First thing we need to do is to create a random elliptic curve. What’s an elliptic curve? Elliptic curves are curves that satisfy the following equation:
y**2 = x**3 + a*x + b
With a and b being real numbers. Although they may sound the same, elliptic curves have little to no relationship to ellipses (AFAIK).
According to wikipedia, we can do this by first choosing a random point (x0, y0) and a random number for the ‘a’ constant. The ‘b’ constant is then calculated:
b = y**2 - x**3 - a*x
This allows us to create a elliptic curve and have a point that is definitely on the curve.
For this algorithm to work, we actually need an elliptic curve of a finite field. You can read about finite fields here. More precisely, let’s say we wanted to find the factors of an integer N. That means our finite field is that of Galois field N (GF(N)). This means our elliptic curve becomes the form:
y**2 ≡ x**3 + a*x + b (mod N)
Part 2: Elliptic curve point addition
A major part in this algorithm is the use of point addition. Smart people have already thought about this, and they have already defined how exactly the point addition takes place. Let’s say we have 2 points on our elliptic curve P (xP, yP) and Q (xQ, yQ) and the expected result is point R (xR, yR). To calculate P + Q = R, we first need to calculate a coefficient λ. According to this wikipedia page, there are two posibilities, either P and Q are different points or they are the same. If they are different points, λ is calculated as follows:
λ = (yQ - yP) / (xQ - xP)
This is for elliptic curve that are not on a finite field. If on a finite field, λ is calculated as follows:
λ ≡ (yQ - yP) * inverse_modulo(xQ - xP, N) (mod N)
The reason being on how the division operation is done on a finite field. If they are the same point, λ is calculated as follows:
λ = (3*xP**2 + a) / yP
For a finite field:
λ ≡ (3*xP**2 + a) * inverse_modulo(yP, N) (mod N)
After calculating lambda, xR and yR are calculated as follows:
xR = λ**2 - xP - xQ ; yR = λ(xP-xR) - yP
Part 3: Elliptic curve multiplication by scalar
For multiplication by a scalar, we can do point addition and doubling to get an efficient O(log k) multiplication, for some scalar k. This trick is similar to fast exponentiation method, so I wont explain how it works
Part 4: The ECM part
Now that we have an elliptic curve, some random valid point P and point addition defined correctly, we need to calculate (B!)*P, with a not too large B. (B!)*P can be calculated efficiently by first calculating 2*P, then 3*(2*P), then 4*(3*(2*P)), and so on. During this process, one of two things will happen:
- A non-invertable point is found during point addition, which means gcd(v, n) != 1 for some v. In this case gcd(v, n) could be n, in which we need to start over again, but of it isn’t we just found a valid factor.
- No non-invertable points are found, so we need to start over with a new random curve.
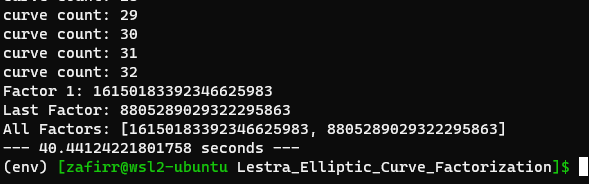
That’s pretty much it. It’s pretty simple, so below is code in python. In there is a semiprime that consists of 2 64-bit primes. My code took around a minute to break it.
NOTE: THIS CODE IS NOT PRODUCTION READY. DO NOT USE IT IN CRYPTOGRAPHIC IMPLEMENTATIONS
import random
import sys
import time
import math
from Crypto.Util.number import isPrime
class EllipticCurveFiniteField:
def __init__(self, x0, y0, a, n):
self.a = a
self.b = y0**2 - x0**3 - a*x0
self.n = n
self.O = "Origin"
def isValidPoint(self, x, y) -> bool:
return (y**2 % self.n) == (x**3 + self.a*x + self.b) % self.n
def __eq__(self, other):
return self.a == other.a and self.b == other.b and self.n == other.n
def __str__(self):
return f'y**2 = x**3 + {self.a}*x + {self.b} (mod {self.n})'
class EllipticCurvePoint:
def __init__(self, curve, x, y):
self.curve = curve
self.x = x
self.y = y
assert curve.isValidPoint(x, y), "Point is not on curve"
def __eq__(self, other):
return self.curve == other.curve and self.x == other.x and self.y == other.y
def __add__(self, other):
assert self.curve == other.curve
# Assume self and other is P and Q, result is R
# Algorithm: https://en.wikipedia.org/wiki/Elliptic_curve#The_group_law
if(self == other):
divisor = inverse_mod(2*self.y, self.curve.n)
s = (3*self.x**2 + self.curve.a) * divisor % self.curve.n
else:
divisor = inverse_mod(self.x - other.x, self.curve.n)
s = (self.y - other.y) * divisor % self.curve.n
xR = (s**2 - self.x - other.x) % self.curve.n
yR = (s*(self.x- xR) - self.y) % self.curve.n
return EllipticCurvePoint(self.curve, xR, yR)
def __mul__(self, k):
assert k >= 0
if(k == 0):
return self.curve.origin
base = EllipticCurvePoint(self.curve, self.x, self.y)
res = EllipticCurvePoint(self.curve, self.x, self.y)
while(not k & 1):
res += res
base += base
k >>= 1
k >>= 1
base = base + base
while(k > 0):
if(k & 1):
res += base
base += base
k >>= 1
return res
def __rmul__(self, k):
return self.__mul__(k)
def __str__(self):
return f"({self.x}, {self.y}) on curve {self.curve}"
def gcd(a, b):
'''Get GCD of a and b'''
if(b == 0):
return a
return gcd(b, a % b)
def egcd(a, b):
if(b == 0):
return a, 1, 0
temp_gcd, temp_x, temp_y = egcd(b, a % b)
y = temp_x - (a // b)*temp_y
x = temp_y
return temp_gcd, x, y
def inverse_mod(a, n):
'''Get Multiplicative modular inverse of a mod n'''
if gcd(a, n) != 1:
raise NoModularInverse(gcd(a, n))
_gcd, x, _y = egcd(a, n)
return x % n
def generate_random_point_and_curve(n):
a = random.randint(1, n)
x0 = random.randint(1, n)
y0 = random.randint(1, n)
curve = EllipticCurveFiniteField(x0, y0, a, n)
point = EllipticCurvePoint(curve, x0, y0)
return point, curve
class NoModularInverse(Exception):
pass
sys.setrecursionlimit(4000)
to_factor = 142207032646172885627320863923329208329
cnt = 1
curve_count = 1
factor_list = []
B = 2000
start_time = time.time()
while True:
point, curve = generate_random_point_and_curve(to_factor)
print(f"curve count: {curve_count}")
curve_count += 1
for i in range(1, B+1):
try:
point = i * point
except NoModularInverse as e:
factor = int(str(e))
if(gcd(factor, to_factor) != to_factor):
print(f"Factor {cnt}: {factor}")
cnt += 1
to_factor //= int(str(e))
factor_list.append(factor)
break
if(isPrime(to_factor)):
break
print(f"Last Factor: {to_factor}")
factor_list.append(to_factor)
print(f"All Factors: {factor_list}")
print("--- %s seconds ---" % (time.time() - start_time))